Regional Mathematics Olympiad 2 Question Paper

1. Let ABC be an acute angled scalene triangle with circumcenter O orthocenter H. If M is the midpoint of BC, then show that AO and HM intersect at the circumcircle of ABC.
2. Let n be a positive integer such that 2n + 1 and 3n + 1 are both perfect squares. Show that 5n + 3 is a composite numbers.
3. Let a, b, c > 0. If 1/a , 1/b and 1/c are in arithmetic progression, and if \(a^2 + b^2 , b^2 + c^2 , c^2 + a^2 \) are in geometric progression, prove that a=b=c.
4. Find the number of 4 digit numbers with distinct digits chosen from the set {0, 1, 2, 3, 4, 5} in which no two adjacent digits are even. 
5. Let ABCD be a convex quadrilateral. Let E, F, G, H be midpoints of AB, BC, CD, DA respectively. If AC, BD, EG, FH concur at a point O, prove that ABCD is a parallelogram.
6. Find the largest real constant \(\lambda\) such that \(\frac{\lambda abc}{a+b+c}\le (a+b)^2 + (a+b+4c)^2\) for all positive real numbers a, b and c.

I.S.I. Entrance Model Test @ Cheenta Schedule

The model test are based on the entrances of Indian Statistical Institute B.Stat and B.Math Entrance which are scheduled on 13th May, 2012.

All Cheenta Model Test will be held on Saturdays. The tests will start at 10 AM in the morning in our Kolkata center.

External Students may also appear in the tests. For registration call 09804005499, 07381944396 or mail us at helpdesk at cheenta dot com.

Model Test	Date
1	17th December, 2011
2	31st December, 2011
3	14th January, 2012
4	28th January, 2012
5	11th February, 2012
6	25th February, 2012
7	10th March, 2012
8	24th March, 2012
9	7th April, 2012
10	21st April, 2012

MATH @ CHEENTA .... PEDAGOGICAL THOUGHTS FOR 2012

The best way to learn mathematics is to DO mathematics. In fact we can add something more to that. The best way to get inspired about mathematics is to 'experience' beautiful mathematics.
In 2012 we are transforming our learning (and teaching) methods. Till today the basic style of our program comprised of:

• Inside Classroom
• a 3.5 hours session
• a diagnosis test in the beginning (25 points; 15 minutes; on the previous day's work)
• topic 1 discussion accompanied by a problem sheet - 1.5 hour
• topic 2 discussion accompanied by a problem sheet - 1.5 hour
• an effect test at the end (25 points; 15 minutes; on the current day's work)
• specification of homework; homework copy submission; returning of previous day's homework copy
• Outside Classroom
• Over phone and internet - round-the week support (our policy is - when a student calls we call back - this saves call charge for the student and allows him/her to discuss freely the queries)
• Continuous interaction with students through social networks and blogs
• Supporting Activities
• Seasonal coming-together where current students and alumni meet.
• Chess tournament, amateur math contests
• Alumni support - we engage with our ex-students in their mathematical pursuits

In 2012 the program will transform into ..

• Inside Classroom
• a 3.5 hours session
• a start-up test in the beginning (20 points; 15 minutes; motivation problem that will lead to current day's discussion)
• a discussion and problem solving session where we 'perform' about 10 olympiad caliber problems - 1.5 hour
• a topic centric discussion session accompanied by necessary problem sheet - 1.5 hour
• an effect test that will simultaneously 'take care of' current session and previous session's discussion
• a light-weight indication of home task; mandatory submission of homework copy; scrutinized homework copies goes back to student
• Outside Classroom
• Over phone and internet - round-the week support (our policy is - when a student calls we call back - this saves call charge for the student and allows him/her to discuss freely the queries)
• Continuous interaction with students through social networks and blogs
• Supporting Activities
• Mathematical Research Cell - Two or three intensive discussion sessions on algebraic geometry, analytical number theory, computer science and other advanced topics to kick-start research activity amongst our alumni (who are pursuing mathematics and computer science related courses at college or university level)
• At least two times a year get-together for current students, alumni and friends of Cheenta.
• Chess Tournaments, Math Contests, Computer Science contests
• Integration of ideas from Physics and Chemistry in the Junior Olympiad level mathematical program to provide an extended exposure to the students
• Full Length Tests on every alternate Saturday (round-the-year).
• Book - Club to share rare books related to Mathematics, Science and Literature

 Please give your suggestions and help us develop a truly world class program.

CLASS PREVIEW: WEEK AHEAD

INSIDE CLASSROOM: WEEK AHEAD

RMO 2011 SOLUTIONS

1. Let ABC be a triangle. Let D, E, F be points on the segments BC, CA and AB such that AD, BE and CA concur at K. Suppose \(\frac{BD}{DC} = \frac{BF}{FA}\) and ∠ADB = ∠AFC. Prove that ∠ABE = ∠CAD.

Solution:

Diagram

Given: ABC be any triangle. AD, BE and CF are drawn from A, B, C to BC, CA and AB respectively such that they concur at K and \(\frac{BD}{DC} = \frac{BF}{FA}\) and ∠ADB = ∠AFC.

R.T.P.:  ∠ABE = ∠CAD;

Construction: FD is joined.

Proof: 

Since ∠ADB = ∠AFC; 
hence 180° - ∠BFC = ∠ADB;
=> ∠BFC + ∠ADB = 180°;
=> BDKF is a cyclic quadrilateral (since sum of an opposite pair of angles 180°)

Hence  ∠FBK = ∠FDK (angles in the segment FK in the cyclic quadrilateral BDKF) .... (i)

Since  \(\frac{BD}{DC} = \frac{BF}{FA}\)
=> DF||AC
=> ∠FDA = ∠CAD (alternate angles)
Since  by (i) ∠FBK = ∠FDK
=> ∠ABE = ∠FBK = ∠FDK = ∠FDA = ∠CAD;
=>  ∠ABE = ∠CAD;

Q.E.D.

2.  Let \(a_1 , a_2 , ... , a_{2011}\) be a permutation of the numbers 1, 2, ..., 2011. Show that there exists two numbers j and k such that \(1\le j < k \le 2011\) and |\(a_j - j\)| = |\(a_k -k\)|

Solution:  
Let |\(a_j - j \)| = \(t_j\)

If all the  \(t_j\)-s are different then they will take up each value from 0 to 2010 (included) exactly once.


squaring both sides and adding all terms we get

\(a_1^2 + a_2^2 + ... + a_ {2011}^2 + 1^2 + 2^2 + ... 2011^2  = 2 a_1  1 + 2  a_2 2 + ... + 2  a_{2011} 2011 + (0^2 + 1^2 + ... + 2010^2)\)

The left hand side of the equality is even and the right side is odd. Hence all the numbers from 0 to 2010 cannot appear as values of the 2011 \(t_j\)-s. Hence there must be repetitions.

Proved.

3. A natural number n is chosen strictly between two consecutive perfect squares. The smaller of these two squares is obtained by subtracting k from n and the larger one is obtained by adding ℓ to n. Prove that n - kℓ is a perfect square. 

Solution:

The the two consecutive squares be \(m^2\) and \((m+1)^2\). 
=> n - k = \(m^2\)  ... (i)
     n + ℓ = \((m+1)^2\) ... (ii)
Adding (i) and (ii) we have  (n+ ℓ) + (n-k) = \(m^2 + m^2 + 2m + 1\)
=> 2n + ℓ - k = \(2m^2 + 2m + 1\)
=> ℓ - k = \(2m^2 + 2m + 1 - 2n\)  --- (iii)
Now
(n-k)(n+ℓ) = \(m^2 \times (m+1)^2\)
Hence \((m^2 + m)^2\)
= \(n^2\) + nℓ - nk - ℓk
= \(n^2\) + n(ℓ-1+1) - nk - ℓk
= \(n^2\) + n(ℓ-1) - nk + n - ℓk
= n(n + ℓ - 1 - k) + n - ℓk 
= n(n + ℓ - k - 1) + n - ℓk 
= n(n + 2\(m^2\) + 2m + 1 - 2n - 1) + n - ℓk  .. (replacing ℓ - k by \(2m^2 + 2m + 1 - 2n\) using --- (iii) )
Thus
n - ℓk
= \((m^2 + m)^2  - n( 2m^2 + 2m - n)\)
= \((m^2 + m)^2  - 2n(m^2 + m) + n^2)\)

=> n - ℓk = \((m^2 + m - n)^2\)

HENCE PROVED that  n - ℓk is a perfect square.

4. K is a 20-sided convex polygon with vertices \(A_1 , A_2 , ... , A_20 \)in that order. Find the number of ways in which three sides of K can be chosen so that every pair among them has at least two sides of K between them. For example \(A_1 A_2\) , \(A_4 A_5\) and \(A_11 A_12\) is a permissible triplet, but  \(A_1 A_2\) , \(A_4 A_5\) and \(A_19 A_20\)  is not.

Solution:

Let us divide the set of 3-sides (such that every pair of them has at least two sides between them) into mutually exclusive and exhaustive subsets. Then we will count the subsets effecting the counting of the entire set.

1. Exactly two sides between one pair of selected sides

The two sides along with the two in-between sides create chain of 4 sides. There are 20 such 4-side-chains: \(s_1 s_2 s_3 s_4\) through \(s_20 s_1 s_2 s_3\) where \(s_i\) denotes a side. Note that in each of those 4-side-chains we have selected the first one and the last one. The two in the middle denote the 'gap'.

The third member of the triplet is yet to be selected. There can be two situations:

a) The third side is at exactly 2-side away from one of the two sides selected. Then we basically have a 7-side-chain in which the first, fourth and the seventh are member of the triplet and rest are acting as gap-sides. There are 20 7-side-chains leading to 20 triplets.

b) Third side is strictly MORE than 2-side away from both of the two sides selected. Then at two ends of a 4-side-chain we leave out three sides more. Hence 4 sides of the 4-side-chain plus six more sides (6 from each end) – in total 10 sides are deducted. The third side must be selected from the remaining 10 sides. This is true for all the twenty 4-side-chains. Hence we get = 200 triplets.

2. Exactly three sides between one pair of selected sides

Similarly we first count 5-side-chains. There 20 such chains. From each chain we take the first and the fifth member for our triplet.

The third member of the triplet can be selected in exactly two ways:

a) The third side is exactly 3-sides away from one of the two selected sides. Then we are basically counting 9-side-chains. There are 20 such chains leading to 20 triplets.

b) The third side is strictly MORE than 3-sides away from both of the selected sides. Hence we leave out 4 sides from each end of the 5-chain. Hence the 3^rd side has to be selected from the remaining 7 sides (20- 5 -4 -4) leading to = 140 triplets.

3. Exactly four sides between one pair of selected sides

First a 6-chain in selected from first and sixth side becomes member of the triplet. Investigation for the third member leads to two cases again.

a) Both gaps are of 4-side length. Hence we count all the 11-side-chains. There are 20 such chains leading to 20 triplets.

b) The third side is strictly MORE than 4 -side away from both of the selected sides. Hence we leave out 5 sides from each end of the 6-chain. Hence the 3^rd side has to be selected from the remaining 4 sides (20- 6 -5 -5) leading to = 80 triplets.

4. Exactly five sides between one pair of selected sides

First a 7-chain in selected from which first and seventh side becomes member of the triplet. Investigation for the third member leads to two cases.

a) Both gaps are of 5-side length. Hence we count all the 13-side-chains. There are 20 such chains leading to 20 triplets.

b) The third side is strictly MORE than 5 -side away from both of the selected sides. Hence we leave out 6 sides from each end of the 7-chain. Hence the 3^rd side has to be selected from the remaining 1 sides (20- 7 -6 -6) leading to = 20 triplets.

Number of triplets= 20 + 200 + 20 + 140 + 20 + 80 + 20 + 20 = 520

ANSWER: 520

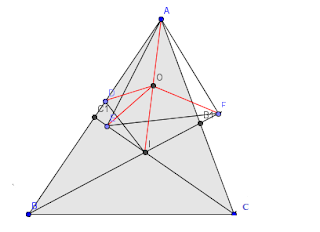
5. ABC is a triangle. \(BB_1\) and \(CC_1\) respectively are the bisectors of ∠B and ∠C with \(B_1\) on AC and \(C_1\) on AB. Let E anf F be the feet of the perpendiculars drawn from A onto \(BB_1\) and \(CC_1\) respectively. Suppose D is the point at which the incircle of ABC touches AB. Prove that AD = EF.

Solution:

Diagram:


Given: ABC be a triangle. \(BB_1\) and \(CC_1\) respectively are the bisectors of ∠B and ∠C with \(B_1\) on AC and \(C_1\) on AB. Let E anf F be the feet of the perpendiculars drawn from A onto \(BB_1\) and \(CC_1\) respectively. Suppose D is the point at which the incircle of ABC touches AB.

Required to Proof: AD = EF;

Construction: Let \(BB_1\) and \(CC_1\) intersect at I which is then the incentre of the triangle. ID is the perpendicular dropped on AB from I. Then ID is an inradius. EF and AI are joined. Let O be the midpoint of AI. OD, OA, OE and OF are joined.


Proof: 


∠ADI = ∠AEI (by given hypothesis both the right angles)
=> A, I, E, D concyclic (since angles subtended by the segment AI at D and E are equal)
=> Also AI is the diameter
Similarly A, I, E and F are concyclic.
But one and only one circle can pass through three non collinear points. Hence only one circle passes through A, I and E.
Hence all the five points A, I, E, D and F are on the same circle which has AI as the diameter.
Since O is the midpoint of AI and AI is the diameter; hence O is the center of the circle through A, D, E, I, F.

In triangle ΔOAD and ΔOEF
OD = OE (radii of the same circle)
OA = OF (radii of the same circle)
∠AOD = ∠EOF = 180° - A (proof of this claim follows)

Hence ΔOAD  ≅ ΔOEF => AD = EF (HENCE PROVED)


Lemma
R.T.P.: ∠AOD = ∠EOF = 180° - ∠A
Proof: ∠AOD = 2∠AID (angle at the circumference is half the angle at the center).

Also ∠AID = 90° - ∠A/2 (since I is the incenter, AI bisects ∠A; hence in ΔADI, ∠ADI = 90°, ∠DAI = ∠A/2; remaining ∠AID = 90° - ∠A/2)

Hence  ∠AOD = 2∠AID = 2(90° - ∠A/2) = 180° - ∠A -- (*)

Again in  ΔIBC, ∠IBC = ∠B/2; ∠ICB = ∠C/2; hence remaining ∠BIC = 180° - (∠B/2+ ∠C/2) = 90° + ∠A/2; Hence ∠EIF = 90° + ∠A/2 (vertically opposite angles);
Hence ∠EAF = 90°- ∠A/2 (Since EAFI is a cyclic quadrilateral, sum of opposite angles ∠EIF and ∠EAF is 180°)
Thus  ∠EOF = 2∠EAF = 180° - ∠A (Since angle at the center is twice the angle at the circumference) -- (**)

Hence from  (*) and (**) we conclude ∠AOD = ∠EOF = 180° - ∠A

Q.E.D. 

6. Find all pairs \((x,y) \in \mathbb{R} \) such that \(16^{x^2 + y} + 16^{x + y^2} \) =1

Solution:

 

Regional Math Olympiad

The Dreams of Pythagoras

Pythagoras is famous. Even those who do not like mathematics, have heard of Pythagoras' Theorem (regarding right angled triangles). He lived about 2500 years ago and did about 2500 wonderful things (well may be a little less) but all that is not the subject matter of this note. We want to talk about the shattered dreams of this famous mathematician and how the pieces of those fragmented dreams created modern mathematics. Pythagoras

Pythagoras believed numbers are omnipotent. The world that we see, the sound that we hear and even the thoughts and emotions that stir our mind are nothing but different numerical expressions of varying complexity. He even produced a theory that 'numerified' the world of music.

Every number, for Pythagoras, originates from 1. 1 was the all powerful number for him. You want to make a 10? Put ten 1's together and you have it. You want to make 3.2? First put three 1's together; that makes a 3. Then break another 'one' into ten equal pieces (each is then of the value 1/10 or 0.1) Put two of those pieces together with the 3 that you made earlier and behold ... you have 3.2.

In this way, claimed Pythagoras, you can make ANY number under heaven.

How can you make 1/3 = 0.3333333333 (and it goes on)? That is easy! Break the piece of '1' into three equal pieces and take one of them. In this way you can make 3.24, 1000, 35.123, 0.6666666 (2/3 - put the length of two 1's side by side, break the length into three equal parts, and you have it!)

The underlying idea of Pythagoras was this: any number is a ratio of two whole numbers (whole numbers being some multiple of 1). Such was the happy world of Pythagoras where every number was invariably extractable from 1.

Then came the NEMESIS... A right angled triangle whose two sides are of one unit length and the third side..... well Pythagoras started to measure it:

He put a '1' unit length on the third side of the triangle. But the side was not fully covered. 'it is greater than 1 unit' he thought, 'but two sticks of 1 unit length would be a little too longer'. So he broke another '1' unit long stick into into 10 equal pieces and found, to his dismay, that four pieces would be a little too short and 5 would be a little to long than the remaining portion.

The third side is then a little greater than
1+ 4* (1/10)  (=1.4)

Pythagoras again took a piece of 1/10 unit length and broke it into 10 parts. Each part is now of 1/100 length. If one of those ten small sticks are added to the remaining part of the third side, a little section still remains uncovered. However if he put two of the small sticks, it would again be a little too longer.

So the third side of the triangle is a little greater than

1+ 4*(1/10) + 1*(1/100) (=1.41)

In this way he tried for some time but it was always either a little more or a little less than the length of the third side. When this practical experiment failed, he tried a mathematical trick. He assumed the third side to be m/n (where m and n are positive integers). After all possible cancellations of common factors amongst numerator and denominator let the final ratio be a/b.

Now the famous Pythagoras' theorem says that the square of the third side is equal to the sum of the squares of other two sides. As the 'other two sides' of our satanic triangle are each one unit long, sum of their squares is 2 (square of 1 is 1 and add to that another square of 1 which is also 1). Hence the square of (a/b) must be 2. Hence after cross multiplication we have

a^2 = 2*b^2

Thus a^2 must be even (since 2*b^2 is a multiple of 2 hence it is even).

Then 'a' must be even. (If a is odd, a*a = a^2 would be odd since odd times odd is odd)

Since 'a' is even, a = 2*t (since 2 is factor of a)

Hence a^2 = (2*t)^2 = 4*(t^2)

Thus 4*(t^2) = 2*(b^2) or b^2 = 2*(t^2)

But then b^2 is even and hence b is even.

But this makes both a and b even which is outrageous because initially we had no common factors amongst a and b (realize that all common factors of m and n are cancelled out to make a/b).

Pythagoras was doubly puzzled. He could not accept the fact that there is no ratio whose square is 2. He could not accept this because then his theory of number would become incomplete and hence no more omnipotent. His belief, his dream about the 'numerified' world would be shattered. When one of his students suggested that such a ratio (whose square is 2) does not exist, he became so angry that he drowned him in the ocean.

However ideas can never be drowned. In modern mathematics, we know that a ratio whose square is 2, does not exist. In fact the number whose square is 2, can never be 'exactly' determined in terms of decimal expression. It is approximately 1.41421356237309504880168872420969807856967187537694807317667973799... (up till 65 digits). But it is a never ending decimal.

Right Books!

This post is mainly for our alumnis - those who have cleared one of the three entrances (Indian Statistical Institute, Chennai Mathematical Institute or Institute of Mathematics and Applications), and pursuing an undergraduate mathematics course.

It is very important to choose the right books. Once you are in college, you may face two kinds of challenges regarding books.

The first is the challenge of plenty. There are thousands of books written on a single topic and your college library will have many of them. Even after a couple of months through a semester you may find yourself shuffling amongst multiple books on a single topic without really 'doing' any one of them.

The second is the challenge of cliche. In India, (and elsewhere in the world), mathematics honors students have some 'cliche' books, or rather 'rule of the thumb' book which are supposed to 'contain all the theorem' and 'exam type exercises'. These books are generally 'manual type' in nature. Since they are devoid of any intuitive discussion (and approach), they are sufficient to destroy independent and creative mathematical thinking (which should be your aim if you have taken up mathematics as your honors).

As a remedy to these challenges we provide 'first layer' and 'second layer' books on five important papers (usually taught in the first semester of a Math Honors undergraduate course).

First Layer

Analysis - Bartley Shebert, Precalculus by Tarasov
Linear Algebra - Bronson De Costa
Probability - Ross
Discrete Mathematics - Rosen
Abstract Algebra - Herstein

Second Layer 

Analysis - Rudin
Linear Algebra - Lang
Probability - Probability through Problems by Marek Capinski
Discrete Mathematics - Krishnamurthy
Abstract Algebra - Artin

Apart from a through reading and problem solving using the above mentioned books, you may also solve the Berkeley Book on Problems. It will help you to perform better in entrances for graduate schools (like TIFR, IMSc, IISc, etc)

Number Theory course - 1.1

We want to develop the most comprehensive, intuitive and exciting number theory course (for mathematics olympiad).

The first step toward that goal is to gather the important books.

1. Mathematical Circles by Fomin
2. Excursion in Mathematics by Bhaskaracharya Pratisthana
3. 104 Number Theory Problems by Titu Andreescu
4. Problem Solving Strategies by Arthur Engel
5. Elements of Number Theory by David Burton

Unfortunately none of the books are 'explicit' as far as the proof of relatively complicated theorems go. For example none of them have 'understandable' or 'intuitive' discussion on the proofs of Chinese Remainder Theorem or Wilson's Theorem. The point is not about 'dumbing down ' the matter. Feynman did not dumb down physics yet he managed to keep it interesting (Ref: Lectures on Physics).

CHEENTA Number Theory course work is split up into 14 sessions. Each session is of 180 minutes or three hours.

1. Session 1 - Mathematical Circles
2. Session 2 - Mathematical Circles
3. Session 3 - Mathematical Circles
4. Session 4 - Mathematical Circles
5. Session 5 - 104 Number Theory Problems
6. Session 6 - 104 Number Theory Problems
7. Session 7 - 104 Number Theory Problems
8. Session 8 - 104 Number Theory Problems
9. Session 9 - 104 Number Theory Problems
10. Session 10 - 104 Number Theory Problems
11. Session 11 - Problem Solving Strategies
12. Session 12 - Problem Solving Strategies
13. Session 13 - Problem Solving Strategies
14. Session 14 - Problem Solving Strategies

We want to solve about 200 (Problem Solving Strategies) + 200 (104 Number Theory Problems) + 150 problems (Mathematical Circles) = 550 problems inside classroom. Elementary Number Theory by Burton will be used as an additional theoretical companion whereas Excursion in Mathematics as an additional problem solving aid.

Please suggest improvements.

a nice problem from ISI 10+2

Compute I = \(\int_e^{e^4}\sqrt{log(x)}dx\) if it is given that \(\int _1^2 e^{t^2} dt = \alpha \)

I = \([x \sqrt{log(x)}]_e^{e^4} - \int_e^{e^4} x \frac{1}{2 \sqrt{log(x)}} \frac {1}{x} dx \)
= \([e^4 \sqrt {log_e e^4} - e \sqrt {log _e e}] - \frac{1}{2} \int_e^{e^4}\frac{1}{\sqrt{log(x)}} dx \)
= \(2 e^4 - e - \frac{1}{2} \int_e^{e^4}\frac{1}{\sqrt{log(x)}} dx \)

let log(x) = \(t^2\)

x =\(e^{t^2}\)

dx = 2t \(e^{t^2}\) dt

Thus I = \(2 e^4 - e - \frac{1}{2} \int_e^{e^4}\frac{1}{\sqrt{log(x)}} dx \)

=  \(2 e^4 - e - \frac{1}{2} \int _1^2 \frac {1}{t} 2 t e^{t^2} dt \)
=  \(2 e^4 - e -  \int _1^2 e^{t^2} dt \)
=  \(2 e^4 - e - \alpha \)

Number Theory Course Revamped

The topics that we learn and teach at CGK are:

• Math Olympiad topics
• Number Theory
• Geometry
• Combinatorics
• Functional Equation
• Inequalities
• Polynomials
• Trigonometry
• Complex Numbers
• High School Topics
• Calculus
• Algebra
• Coordinate Geometry
• Trigonometry
• Symbolic Logic
• Computer Science (C language)

We have stand alone courses on each sub topic. These stand-alone courses together make the entire mathematics program at Cheenta Ganit Kendra. Apart from the stand alone courses we have high intensity (inter-topic or topic-introducing) seminars which make the mathematics program worth experiencing.

NUMBER THEORY

As far as number theory is concerned, we have revamped the entire course. The course roughly constitutes.

Content

1. Divisibility 1 and 2 from Mathematical Circles Russian Experience - 4 problem sheets
2. Mathematical Induction and Binomial Theorem - 2 problem sheets
3. 104 Number Theory Problems - 4 problem sheets
4. 105 Diophantine Equation - 4 problem sheets
5. Number Theory section of Problem Solving Strategies by Arthur Engel - 4 problem sheets
6. Navigation through David Burton's Elementary Number Theory - 4 problem sheets

Power-seminars

1. Geometry inside congruency - 2 hours

Time-Line

Each problem sheet may take 5 hours of classroom work. The entire number theory course will be accomplished in 100 hours.

ISI 2013 Batch, 18th September Class Preview

ISI 2013 Class Preview

class preview - 4th september EARLY BIRD OLYMPIAD

TARGET ISI 2013 (AFTERNOON) 21st AUGUST Sunday, CLASS PREVIEW

We are currently working on Number Theory and Coordinate Geometry. On 21st August, the TARGET ISI 2013  session will be something like this:

1. 1:30 PM - Class begins with a 15 minutes test on Number Theory and Coordinate Geometry. It will cover whatever we learnt in the previous classes
2. 1:45 PM - The first section on coordinate geometry will resume. We will continue with the Analytical Geometry - 1 Sheet. This section will run for 1 hour 15 minutes. We hope to cover much of straight lines.
3. 3:00 PM - We will have a break of 10 minutes. This week we again have the HAVE A BREAK pamphlet. We also have fresh coffee.
4. 3:15 PM - The second section on Number theory begins. Apart from discussing the Number Theory - 1 in detail we want to introduce the Chinese Remainder Theorem in this class. This section will also run for 1 hour 15 minutes.
5. 4:30 PM - The Effect Test begins (and it will run for 15 minutes).
6. 4:45 PM - Class concludes, students submit homework copies, take back corrected ones.

EARLY BIRD (MORNING) 21st AUGUST Sunday, CLASS PREVIEW

We are currently working our way through number theory and geometry. We had brief experience of combinatorics in June.
On 21st August, the early bird olympiad batch will be something like this:

1. 10:15 AM - Class begins with a 15 minutes test on Number Theory and Geometry. It will cover whatever we learnt in the previous classes. For example it will consist of preliminary divisibility problems, geometry problems related to straight lines and parallel lines.
2. 10:30 AM - The first section on geometry will resume. We will continue with the Geometry - 1 Sheet. We will also introduce the problem set from Excursion in mathematics. This section will run for 1 hour.
3. 11:30 AM - We will have a break of 10 minutes. This week we again have the HAVE A BREAK pamphlet. We also have fresh coffee.
4. 11:45 AM - The second section on Number theory begins. Apart from discussing the Number Theory - 1 in detail we want to introduce the Chinese Remainder Theorem in this class. This section will also run for 1 hour.
5. 12:45 PM - The Effect Test begins (and it will run for 15 minutes).
6. 1 PM - Class concludes, students submit homework copies, take back corrected ones.

ISI 2012 batch - 17th July Sunday, Evening ; CLASS PREVIEW

We are in mid-July. We have completed the first diagnostic test (I.S.I. B.Math level). We are about to commence the most serious journey through high school mathematics. At this juncture the 17th July class becomes relevant.

The main topics due are:

1. B.Math 2009 last five problems discussion.
2. RMO 1996 concluding part
3. M.L.Khanna Problem Set 63 concluding part
4. Geometry Sheet 1 concluding part

Apart from the above discussion we will have the the DIAGNOSIS TEST and the EFFECT TEST as usual. The "HAVE A BREAK" refresher is also ready to roll.
We have less than 300 days left (about 290 days). What should be our strategy?
By end august (that is in 6 more classes) we should be through with Integral Calculus in it's entirety. Also in 6 classes we will cover the Geometry portion (as far as math olympiads can take us).
September and October will be devoted to Differential Calculus. In the olympiad frontier we will master number theory and combinatorics.
November and December will be devoted to Binomial Theorem, Complex Number, Infinite Series. In the olympiad arena we will face inequality and functional equations (we have RMO in December).
January and February will be devoted to Trigonometry and Coordinate Geometry alone. Olympiad related topics will be suspended (except for those who will crack RMO in December).
March will see Theory of Quadratic Equations in full action. Apart from that we may take up some residual topics. We will enter revision exercises.
So far this is the plan. If you have any suggestion feel free to mail us at helpdesk at cheenta dot com.

10th July 2011 PREVIEW (class XII evening)

The class will start precisely at 5 PM. The basic topics to be covered are:

1. RMO 1997 paper
2. Integral Calculus Concept Building continued (Apostol Ch.1)
3. Passage 64 -67 from M.L.Khanna - 25 problems.
4. Geometry sheet 2

We will have diagnosis test and effect test.

Homework:

1. Calculus M.L. Khanna Passage till Passage 67
2. Geometry - exercises from challenges and thrills of pre-college mathematics (Ex. 3.4 to 3.6)
3. RMO 1998

10th July 2011 PREVIEW (class XI afternoon)

The class will start precisely at 1:30 PM. The basic topics to be covered are:

1. RMO 1993 paper
2. Trigonometry Problem Solving - 25 problems from passage 33 to 34 of M.L. Khanna
3. Inequality Sheet 

We will have diagnosis test and effect test.

Homework:

1. Calculus M.L. Khanna Trigonometrical Identities Complete (Trigonometry) and TMH Trigonometry first chapter taken up
2. Inequality - exercises from challenges and thrills of pre-college mathematics and arthur engel
3. RMO 1994